コグノスケ

未来から過去へ表示(*) link

過去から未来へ表示

もっと前

2014年11月25日 >>> 2014年11月12日

もっと後

2014年11月25日

permalink

編集する

DA変換の続き

目次: PC

前回の日記（2014年11月20日の日記参照）の続きです。

サンプリング周波数（以降fsと書く）の1/6や1/8の周波数を持った矩形波のLPCMデータをDA変換したらどんな波形になりますか？を計算しています。

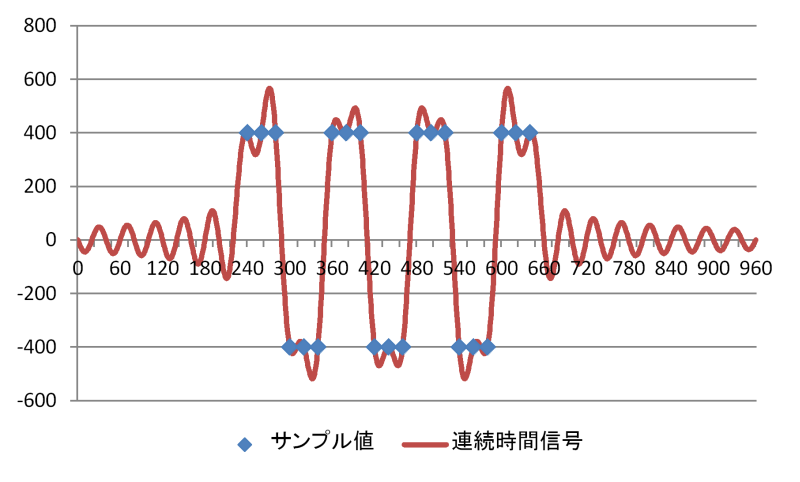
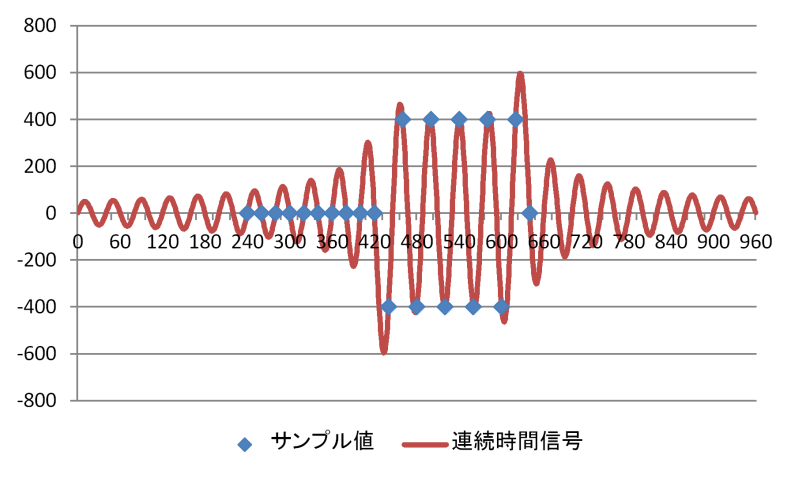
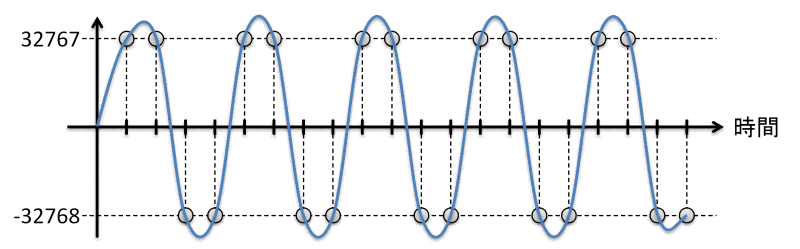
周波数1/6 fsの矩形波のLPCMサンプルデータと連続時間信号

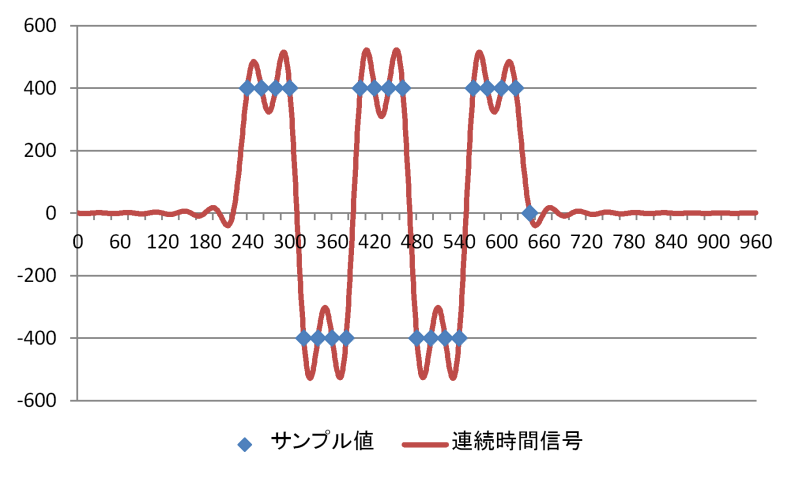
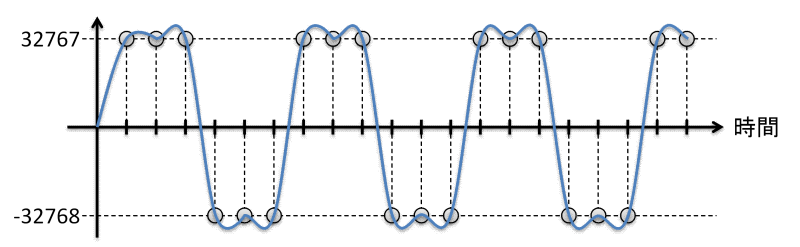
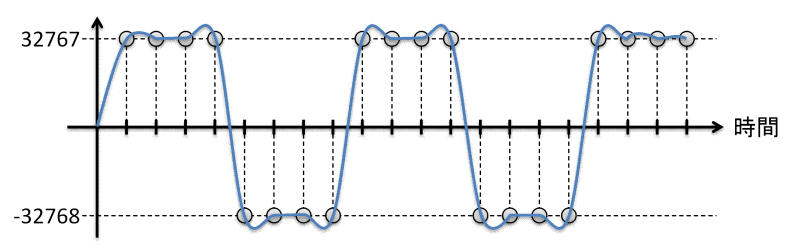
周波数1/8 fsの矩形波のLPCMサンプルデータと連続時間信号

前々回に掲載したUSB-DACの出力波形と比べてみても、形が似ていることがわかると思います。

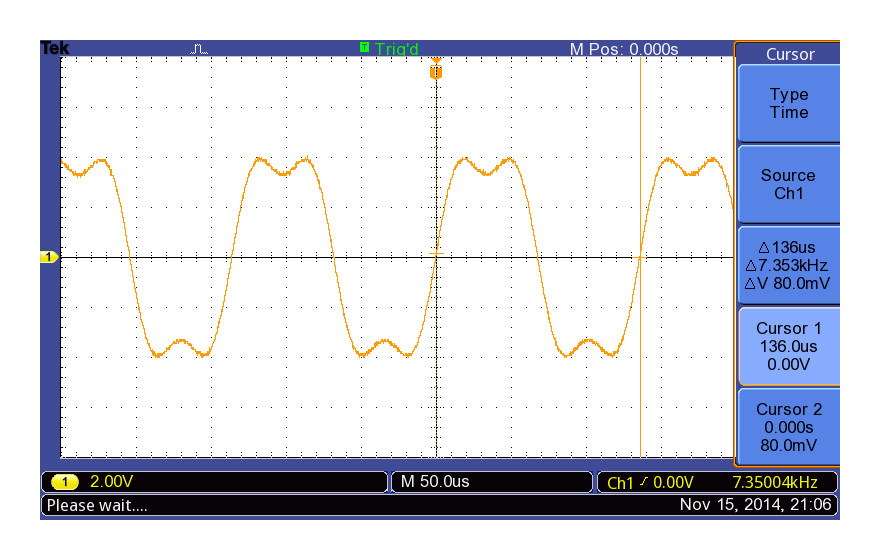
ONKYO SE-U33GXV2の1/6 fs = 7.4kHz矩形波出力（fs = 44.1kHz）（再掲）

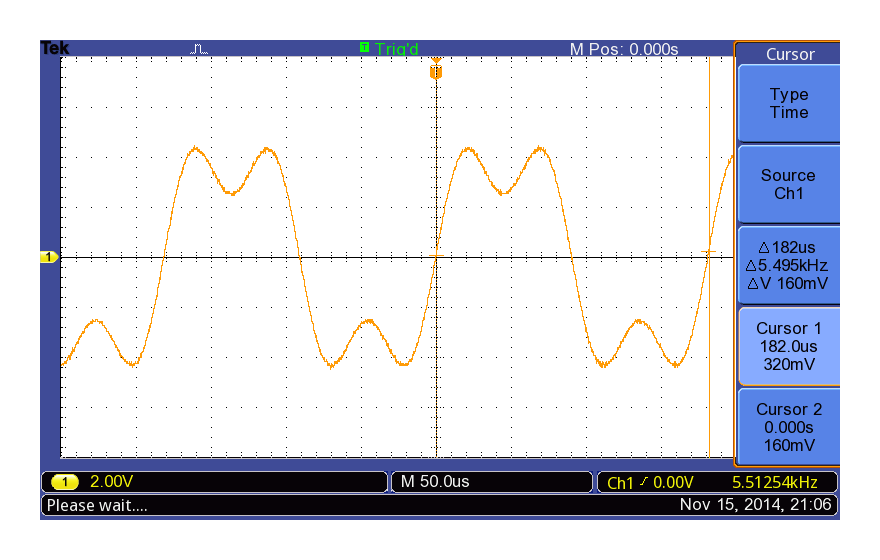
ONKYO SE-U33GXV2の1/8 fs = 5.5kHz矩形波出力（fs = 44.1kHz）（再掲）

当然ながらONKYO SE-U33GXV2は信号発発生器ではないので、波形が歪んでいても文句は言えません。しかし素人が見たり測ったりする限りでは、波形の歪みもなく、ノイズも少なく、基本に忠実なDACです。今更ながら、良い買い物だったなあ、と思います。

そう思うなら、オシロに繋いでないで音楽聴けよって？ええ、ええ、わかってますとも。

理想と現実

計算に使ったsinc関数（sin(x) / x形の関数のこと）は、やっかいなことに無限の過去から無限の未来まで値を持ちます。そのため、あるサンプルの値を変えると、過去から未来の全ての計算結果に対して影響が出ます。

下記グラフのようにLPCMデータ上は0でも、未来のデータの影響を受けるため、0ではないレベルの信号が出力されてしまいます。

周波数1/2 fsの連続時間信号の鳴り始め

無限に影響が出るとは言ってもこの世の機械では計算ができませんので、実際に売られているDACなどの機器ではどこかで影響を打ち切っていると思われます。もしくは思い切って信号の再現性は捨ててsinc関数を使わずに計算しているはずです。

じゃあ実際、どの辺まで計算しているんでしょうね？USB-DACの鳴り始めの信号にトリガを掛けて、オシロスコープで見てみましょう。

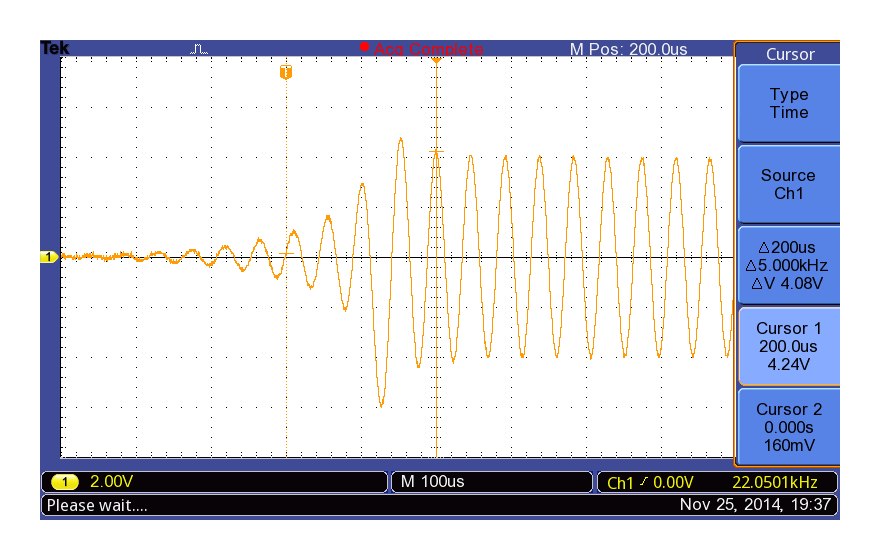
ONKYO SE-U33GXV2の周波数1/2 fs = 22kHzの連続時間信号の鳴り始め（fs = 44.1kHz）

なお、計算値（-400〜 +400）と対応が取りやすいように、いずれのUSB-DACの振幅も-4V〜+4Vの振幅になるように音量を調整しています。

マイナス側に一番大きく-6Vくらいまで振れている波が、一番最初のLPCMデータに対応した信号になります。計算したグラフと見比べるとわかりやすいです。

最初の波より前についても、計算したグラフの形と、オシロスコープの波形がほぼ一致していますので、LPCMデータを入力していない部分は、値0のLPCMデータとして扱っていると見て問題なさそうです。

セカンドオピニオンとしてCreative X-Fi Go! Proにも登場いただくことにします。前々回泣かされたCreative SB Play! とは違って、X-Fi Go! ProのSin波は非常に綺麗です。

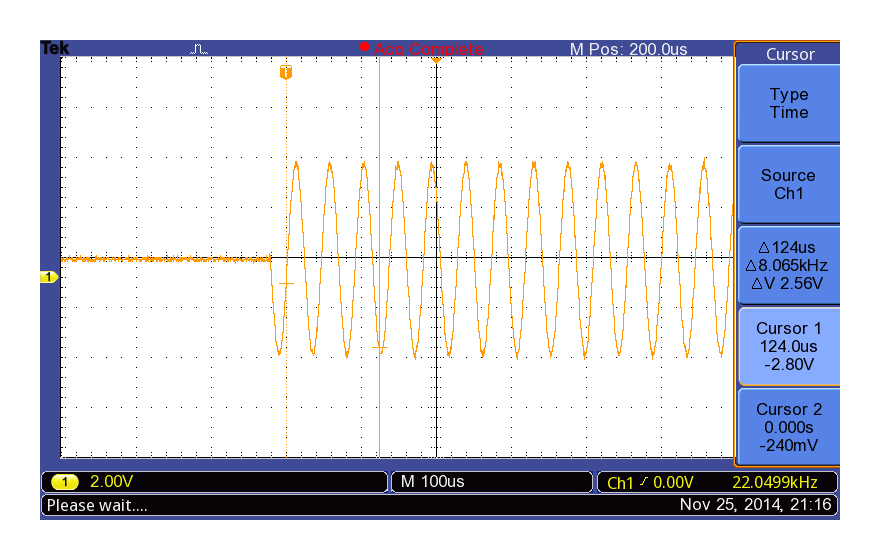
Creative X-Fi Go! Proの周波数1/2 fs = 22kHzの連続時間信号の鳴り始め（fs = 44.1kHz）

なんとなく鳴り始めを打ち切ったような波形ですね。残念ながらセカンドオピニオンならず。せっかく買ったのにションボリですね…。

過去への影響と遅延

オシロスコープの波形と、0データとの交点を数えてみると、下記のように少なくとも鳴り始めより17〜18個前のサンプルまで影響を及ぼしているように見えます。

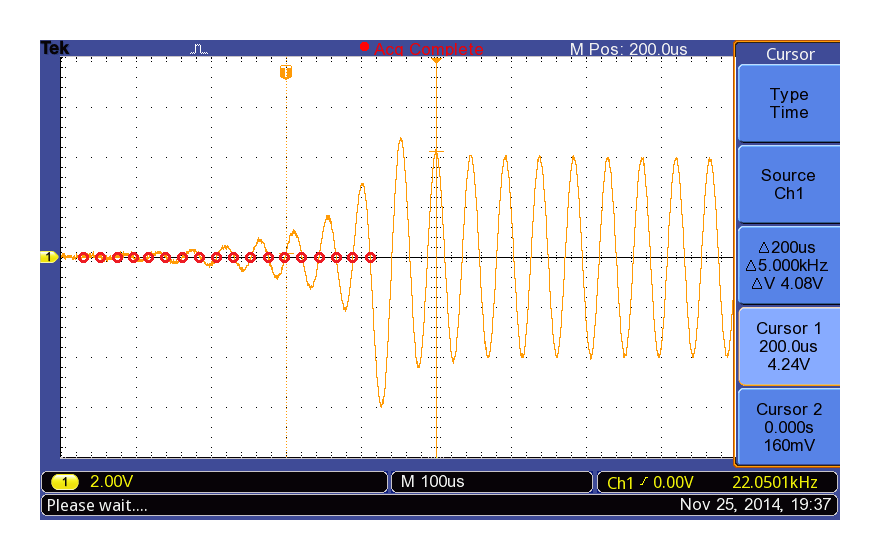
ONKYO SE-U33GXV2の鳴り始め以前の0との交差部分

これは少なくとも18サンプル以上DAC内部に貯めてから、信号の値を計算していることの現れです。たくさん貯めてから計算するほど理想のDA変換に近づきますが、貯めすぎればDACの処理遅延に繋がり、使い勝手は悪くなります。

ちなみに18サンプルの遅延はfs = 44.1kHzのとき、わずか0.408 [ms] に過ぎません。ざっとこの10倍〜20倍のサンプルを貯めてから計算しても、人間に全くわからないレベルの遅延に収まるでしょう。

恐らくUSB-DACはもっとたくさんのサンプルを貯めていて遅延も大きいはずですが、今持っている測定手段ではこれ以上の精度で信号が読めないので、真実については何とも言えませんねー……。

もっと良い測り方をご存じの方は教えていただけると嬉しいです。手持ちの機材で測れそうなら試してみます。

編集者:すずき(2024/10/25 02:00)

コメント一覧

コメントはありません。

この記事にコメントする

2014年11月20日

permalink

編集する

DA変換

目次: PC

前回の日記（2014年11月15日の日記参照）では、DA変換を理解できていなくて、いい加減な図を描いてしまったので、今日はLPCMのサンプル値から連続時間信号を生成した場合の波形を計算して描いてみようと思います。

調べたところによれば、サンプル値x[n] を離散時間フーリエ変換し、周波数領域に変換して、得られた周波数領域のうち角周波数 -π/Ts < ω < π/Tsのみを残すローパスフィルタを掛け（※）、残った周波数領域を逆フーリエ変換すると連続時間信号になるそうです。

（※）Tsはサンプリング周期、つまり何秒に1回サンプリングするかを表す記号です。

計算をすっ飛ばして結果だけ言うと、時間をTsずつずらしながら各サンプル値x[n]とsinc関数（理想的なローパスフィルタを逆フーリエ変換するとsinc関数になる）の積を取り、全て足し合わせれば連続時間信号になります。何故なのか説明できるほど理解できていませんが、ひとまずそういうモンとして計算します。

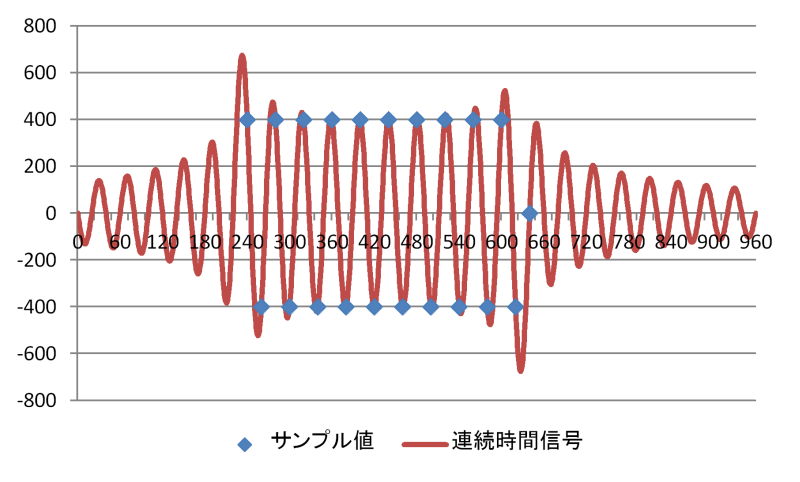
周波数1/2 fsの矩形波のLPCMサンプルデータと連続時間信号

サンプル値は-400から400で、サンプリング周期Tsは20 [s]、サンプリング周波数fsは1/20 = 0.05 [Hz] とし、0〜960 [s] までを計算しています。横軸tの単位は [s] です。

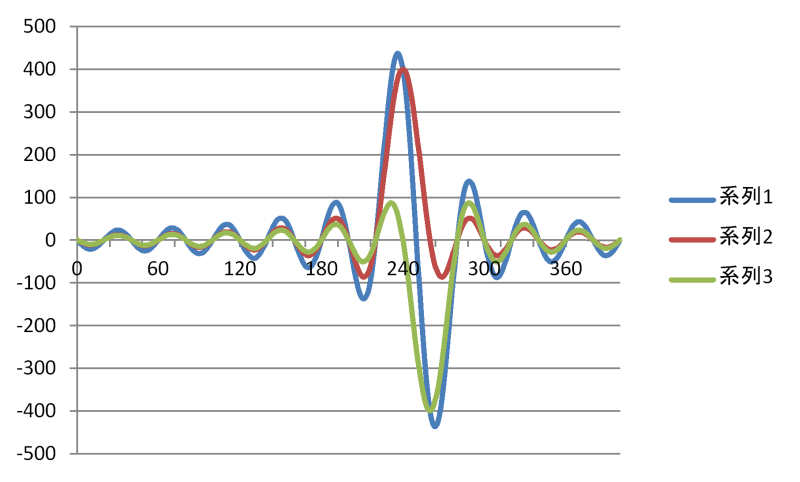
これだけだと「ふーん……？」で終わるので、わかりやすいように1個目のサンプルと、2個目のサンプルのみで、連続時間信号を計算してみます。

各LPCMサンプルデータと対応するsinc関数

赤色（系列2）が1個目のサンプル、緑色（系列3）が2個目のサンプル、青色（系列1）が総和です。1/2 fsかつ、ピーク値がLPCMのサンプル値とほぼイコールのSin波が計算されるのがわかると思います。

じゃあ1/4 fsは？こうなります。

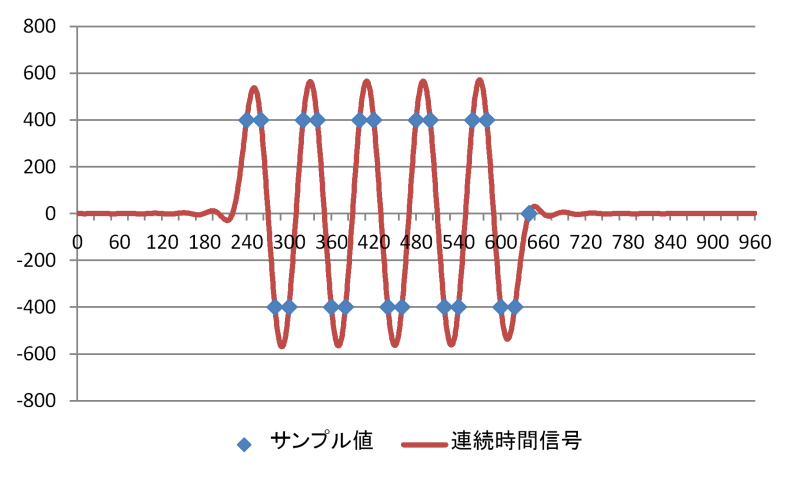
周波数1/4 fsの矩形波のLPCMサンプルデータと連続時間信号

前回の適当な図とは違い1/4 fsのSin波が出力され、ピーク値はLPCMのサンプル値を超えてしまう様子もよくわかると思います。ちなみに連続時間信号のピーク値はt=409（真ん中の山の頂点）で563.7です。

もちろん1/6 fsや1/8 fsも計算可能ですが、長くなってきたのでまた後日にでも載せます。

編集者:すずき(2024/10/25 02:02)

コメント一覧

コメントはありません。

この記事にコメントする

2014年11月15日

permalink

編集する

USB-DACと矩形波

目次: PC

前回はSin波を見ました（2014年10月18日の日記参照）が、今回は矩形波を見てみようと思います。

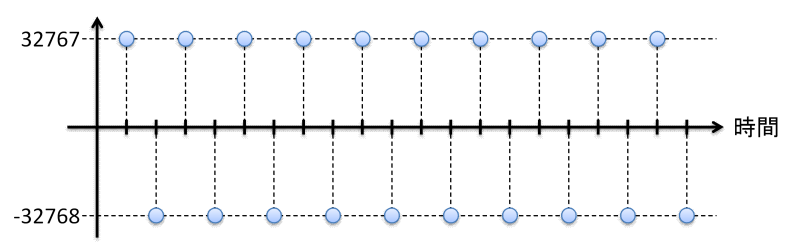
サンプリング周波数の1/2の周波数（以降、1/2 fsと書きます）の矩形波のLPCMデータを下記のように表すとします。

周波数1/2 fsの矩形波のLPCMデータ

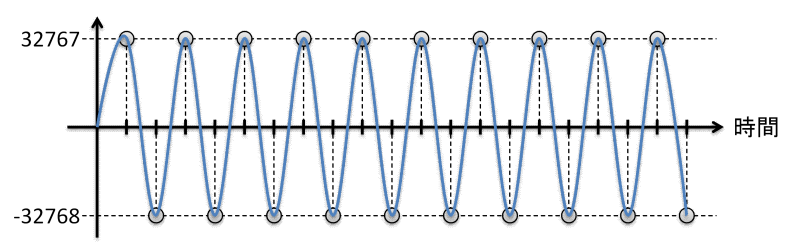
矩形波と書きましたが、このデータをアナログに変換しても矩形波にはなりません。下記のような22kHzのSin波になります。

周波数1/2 fsの矩形波をアナログに変換

私もそれほど詳しくはありませんが、標本化定理と言って、ある波形をサンプリング周波数44kHzでサンプリングした際に完全に元の波形に戻せるのは1/2 fs未満、つまり22kHzまでの周波数を持った波形です。それ以上は情報が失われ、元に戻せません。

見た目は周波数22kHzの波形に見える矩形波でも、波形の立上がり、立下りの部分に高い周波数を含んでいて、この部分が失われてしまうため、元に戻らないのです。

同じ理屈で1/4 fsの矩形波、つまり44kHzのサンプリング周波数で、11kHzの矩形波を表そうとしても、立上がり、立下りの部分が失われ、11kHzのSin波になります。LPCMデータの最大値は変わりませんが、22kHzの時より振幅が大きくなるのが面白いですね。

周波数1/4 fsの矩形波をアナログに変換

見た目が矩形波らしくなるのは1/6 fsか1/8 fsくらいでしょうか。つまり44kHzのサンプリング周波数で、7.4kHzか5.5kHzの矩形波を表そうとしたときです。

周波数1/6 fsの矩形波をアナログに変換

周波数1/8 fsの矩形波をアナログに変換

実際やってみましょう

では、下記のLPCMデータを使ってUSB-DACで再生してみます。

各種揃えましたが、訳あって、この中からサンプリング周波数44kHzのデータを使うことにします。まずは1/2 fsから。

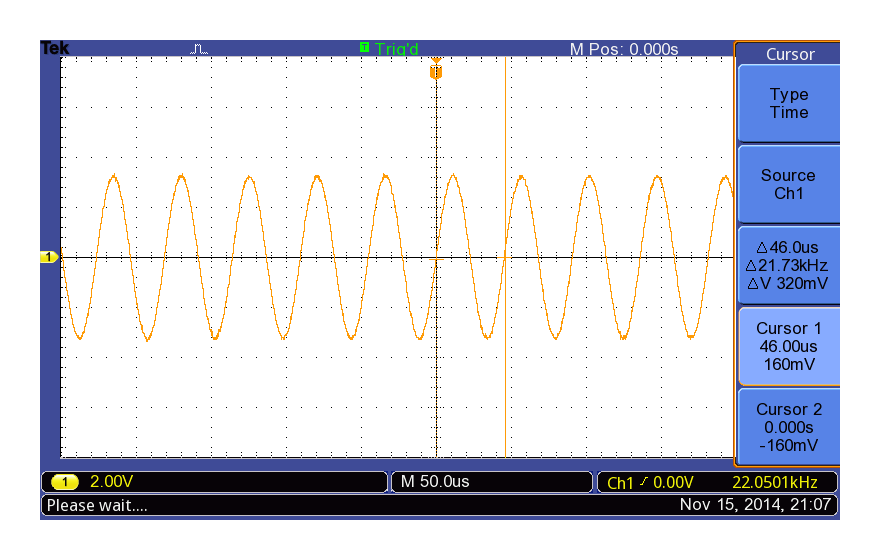
ONKYO SE-U33GXV2の22kHz矩形波出力（fs = 44.1kHz）

綺麗なSin波です。次は1/4 fsです。

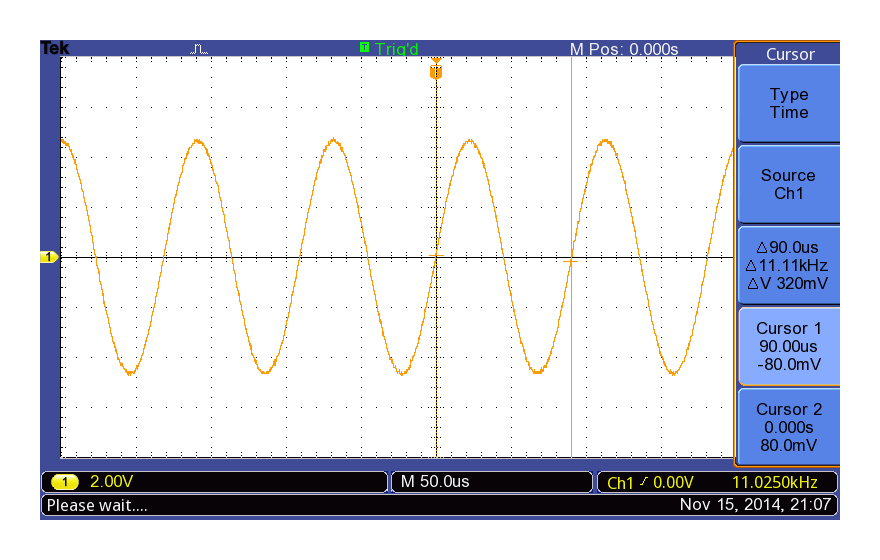
ONKYO SE-U33GXV2の11kHz矩形波出力（fs = 44.1kHz）

これも綺麗なSin波ですね。振幅が先ほどより大きいのがわかると思います。次は1/6 fsと1/8 fsです。

ONKYO SE-U33GXV2の7.4kHz矩形波出力（fs = 44.1kHz）

ONKYO SE-U33GXV2の5.5kHz矩形波出力（fs = 44.1kHz）

角の部分はまだガタガタしていますが、矩形波らしくなってきたのがわかります。

編集者:すずき(2024/10/25 02:03)

コメント一覧

すずきさん(2014/11/19 02:30)
DA 変換を調べていたら、どうも、図のような補完でリンギングが起きているわけではなさそうです。信号処理は難しいな…。

この記事にコメントする

もっと前

2014年11月25日 >>> 2014年11月12日

もっと後

管理用メニュー

記事を新規作成

RSSを更新

<	2014					>
<<	<	11			>	>>
日	月	火	水	木	金	土
-	-	-	-	-	-	1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	-	-	-	-	-	-

本日の日記へ

最近のコメント5件

24年10月1日
すずきさん (10/06 03:41)
「xrdpで十分動作しているので、Wayl...」
24年10月1日
hdkさん (10/03 19:05)
「GNOMEをお使いでしたら今はWayla...」
24年10月1日
すずきさん (10/03 10:12)
「私は逆にVNCサーバーに繋ぐ使い方をした...」
24年10月1日
hdkさん (10/03 08:30)
「おー、面白いですね。xrdpはすでに立ち...」
14年6月13日
2048player...さん (09/26 01:04)
「最後に、この式を出すのに紙4枚(A4)も...」

もっとみる

最近の記事20件

24年10月28日
すずき (10/30 23:49)
「[Linuxからリモートデスクトップ] 目次: Linux開発用のLinuxマシンの画面を見るにはいろいろな手段がありますが、...」
23年4月10日
すずき (10/30 23:46)
「[Linux - まとめリンク] 目次: Linux関係の深いまとめリンク。目次: RISC-V目次: ROCK64/ROCK...」
24年10月24日
すずき (10/25 02:35)
「[ONKYOからM-AUDIOのUSB DACへ] 目次: PCかれこれ10年以上（2013年3月16日の日記参照）活躍してく...」
24年7月25日
すずき (10/25 02:24)
「[OpenSBIを調べる - デバイスツリーの扱い（別方法）] 目次: LinuxOpenSBIのブート部分を調べます。Ope...」
24年8月7日
すずき (10/25 02:23)
「[Debian独自の挙動をするQEMUとbinfmt_misc] 目次: Linux前回はbinfmt_miscの使い方や動作...」
24年9月9日
すずき (10/25 02:22)
「[GDBの便利コマンド] 目次: LinuxGDBは便利ですが、少し使わないでいるとあっという間にコマンドを忘れます。便利＆使...」
24年10月20日
すずき (10/25 02:22)
「[ゲームを買ったら遊びましょう2] 目次: ゲーム前回の振り返り（2022年5月13日の日記参照）から2年半経ちました。所持し...」
24年8月2日
すずき (10/25 02:21)
「[Debian on RISC-V] 目次: LinuxOpenSBI + Linuxの環境まで動いたので、次はLinuxのデ...」
24年8月6日
すずき (10/25 02:21)
「[他アーキテクチャ向けバイナリを実行する仕組みbinfmt_misc] 目次: LinuxRISC-V 64bit用の実行ファ...」
24年8月27日
すずき (10/25 02:20)
「[Milk-V Jupiterが届いた] 目次: RISC-VMilk-V Jupiterが届きました。お値段が非常に安かった...」
24年9月13日
すずき (10/25 02:20)
「[OpenSBIを調べる - OpenSBIとRISC-V ISA extensions] 目次: Linux今回はOpenS...」
24年10月11日
すずき (10/25 02:19)
「[企業のドメイン] 今の企業は公式サイトを持っていなほうが珍しいと思いますが、ドメイン名の使い方は各社でバラバラで面白いです。...」
24年10月21日
すずき (10/25 02:18)
「[OpenPilotを調べる - プロセス間通信msgqの仕組み] 目次: OpenPilot最近はOSSの運転支援ソフトウェ...」
24年10月6日
すずき (10/25 02:11)
「[OpenPilotを調べる - ビルドと実行] 目次: OpenPilot最近はOSSの運転支援ソフトウェアOpenPilo...」
24年7月13日
すずき (10/25 02:10)
「[RISC-V 64向けLinuxブートローダー（OpenSBI）の構築] 目次: Linux以前、Berkeley Boot...」
24年7月19日
すずき (10/25 02:09)
「[OpenSBIを調べる - ブート処理とペイロード] 目次: LinuxOpenSBIのブート部分を調べます。OpenSBI...」
24年7月23日
すずき (10/25 02:08)
「[OpenSBIを調べる - QEMUのデバイスツリー] 目次: LinuxOpenSBIのブート部分を調べます。OpenSB...」
24年7月24日
すずき (10/25 02:08)
「[OpenSBIを調べる - デバイスツリーの扱い（genericプラットフォーム）] 目次: LinuxOpenSBIのブー...」
24年6月27日
すずき (10/25 02:07)
「[何もない組み込み環境でDOOMを動かす - その4 - 自作OSの組み込み環境へ移植] 目次: RISC-V目次: 独自OS...」
24年6月24日
すずき (10/25 02:06)
「[何もない組み込み環境でDOOMを動かす - その1 - 準備編] 目次: RISC-VみなさまはDOOMをご存じでしょうか？...」