2023年3月3日
Dockerのお掃除コマンド
目次: 自宅サーバー
Dockerを使っていると要らなくなったイメージ、コンテナ、ビルドキャッシュがたまってきて、/varディレクトリ以下が肥大化していることがあります。いつも忘れてしまうお掃除用のコマンドをメモしておきます。
各種お掃除方法と確認方法
### 終了しているcontainerの削除 $ docker container prune ### 確認 $ docker container ls -a ### タグもなく使われていないimageの削除 $ docker image prune ### 確認 $ docker image ls -a ### build cacheの削除 $ docker builder prune ### 確認 $ docker builder ls
Dockerがディスク容量をどの程度使用しているのかについてはsystem dfが便利(docker system dfのマニュアル)です。
使用済みディスク容量の確認
$ docker system df TYPE TOTAL ACTIVE SIZE RECLAIMABLE Images 1 1 14.26GB 0B (0%) Containers 2 1 0B 0B Local Volumes 0 0 0B 0B Build Cache 17 0 0B 0B
昔はコマンドの名前に一貫性がなかった記憶がありますが、今はxxx lsとすれば大抵の場合は一覧が出るため統一感があります。私のようなライトユーザーがやりたいと思う程度の機能は、大抵既に存在しており良くできていてありがたいです。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2023年2月28日
SIMDを使ったお手軽最適化 - その2
目次: ベンチマーク
お手軽最適化のメモ、昨日の続きです。行列の掛け算を題材にします。前回は行列の掛け算と素朴な実装のコードを紹介しました。今回はお手軽最適化を紹介します。
スカラー処理だと遅いけれど、お手軽に最適化(数倍程度)がしたいときの参考になれば幸いです。
お手軽コース - 自動ベクトル化
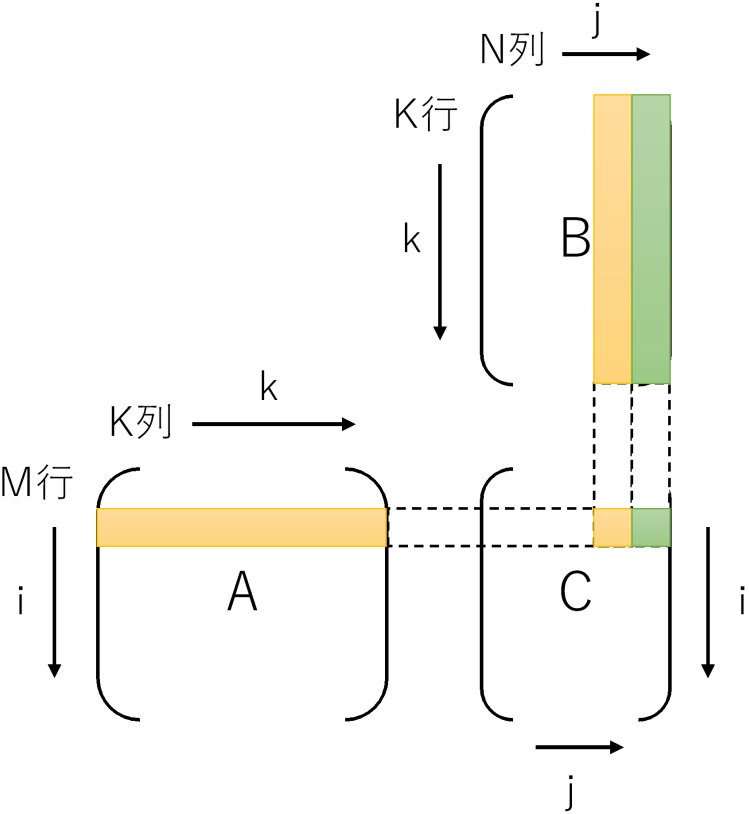
素朴版のコードですとi, j, kの順でループになっていて、kを最内ループにしていました。ループ内の計算は、
ループ内の計算式
c[i * nn + j] += a[i * kk + k] * b[k * nn + j]
でした。このときメモリアクセスのパターンは、
- A: 行方向に連続(メモリアクセスパターンは連続 = 自動ベクトル化できる)
- B: 列方向に連続(メモリアクセスパターンは飛び飛びアクセス = 自動ベクトル化できない)
- C: 同一要素を何度もアクセス
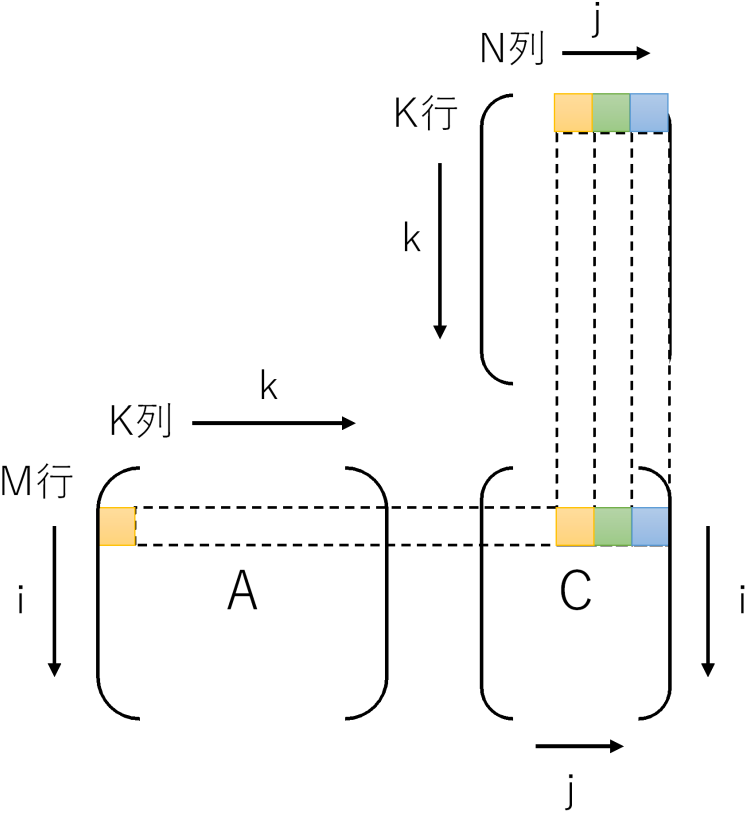
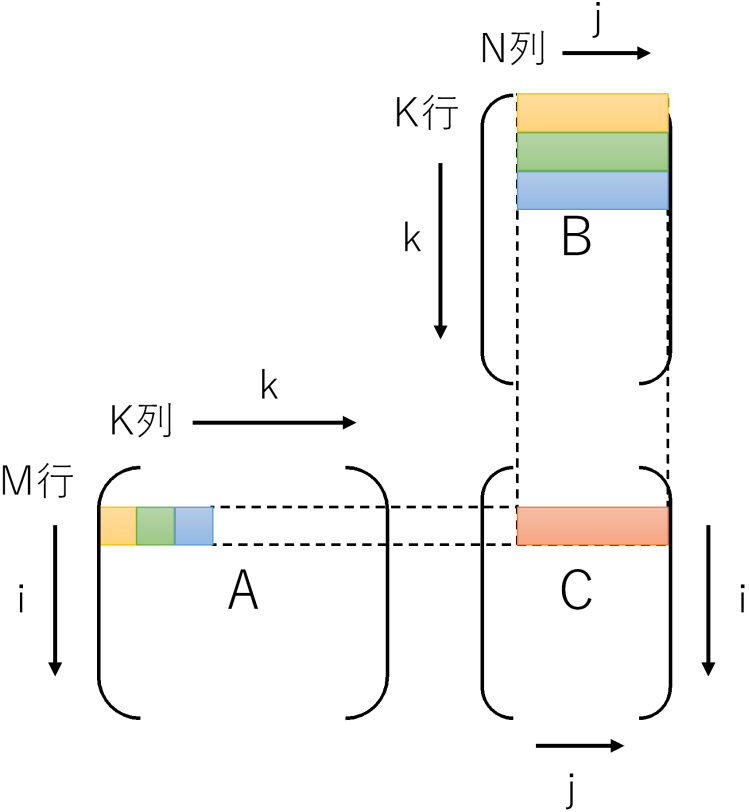
です。GCCの自動ベクトル化ですと、このアクセスパターンをうまく最適化できないようです。対象が最内ループのみなのかもしれません。ループを入れ替えjを最内にして、BとCを行方向に読むようにします。するとメモリアクセスのパターンは、
- A: 同一要素を何度もアクセス
- B: 行方向に連続(メモリアクセスパターンは連続 = 自動ベクトル化できる)
- C: 行方向に連続(メモリアクセスパターンは連続 = 自動ベクトル化できる)
です。ループを入れ替えるとループ内でCの0初期化ができないので、ループの外に追い出して最終的に下記のようなコードになります。
SGEMMループ入れ替え版
void sgemm_inner(const float *a, const float *b, float *c, int mm, int nn, int kk)
{
for (int i = 0; i < mm; i++) {
for (int j = 0; j < nn; j++) {
c[i * nn + j] = 0.0f;
}
}
for (int i = 0; i < mm; i++) {
for (int k = 0; k < kk; k++) {
for (int j = 0; j < nn; j++) { //★★jが最内ループ★★
c[i * nn + j] += a[i * kk + k] * b[k * nn + j];
}
}
}
}
SGEMMループ入れ替え版の実行時間
$ gcc -Wall -g -O2 -fno-tree-vectorize -static -march=znver3 sgemm.c $ ./a.out matrix size: M:1519, N:1517, K:1523 time: 1.528314 (参考: 素朴版の実行時間) time: 2.277758 (参考: OpenBLASシングルスレッドの実行時間) $ export OPENBLAS_NUM_THREADS=1 ----- use CBLAS verify: 0.052149
ループ入れ替えで倍くらい速くなっていますが、この最適化の本領はコンパイラの自動ベクトル化です。GCCならば -ftree-vectorizeオプションを指定すると、行列Bと行列CへのアクセスにSIMD命令を使うようになります。
Ryzen 7 5700Xの場合はAVX2命令を使えます。他のCPUをお使いの場合は -marchを適宜変更してください。
SGEMMループ入れ替え版+自動ベクトル化の実行時間
$ gcc -Wall -g -O2 -ftree-vectorize -static -march=znver3 sgemm.c $ ./a.out matrix size: M:1519, N:1517, K:1523 time: 0.181133 (参考: OpenBLASシングルスレッドの実行時間) $ export OPENBLAS_NUM_THREADS=1 ----- use CBLAS verify: 0.052149
素朴版とOpenBLASでは1/43もの差がありましたが、ループ入れ替えと自動ベクトル化によってOpenBLASの1/3.5程度まで近づきました。GEMMが計算偏重の処理で最適化の効果が出やすい、という点を考慮する必要はあるものの僅かな書き換えで得られる効果にしては割と良いのではないでしょうか。
もう少し頑張るコース - intrinsics
ソースコードを書き換える元気があれば、別の最適化方法もあります。GEMM特有の話に近付いてしまい、汎用的な話から遠ざかりますが、最適化ポイントの例という意味では参考になるはず……です。たぶん。
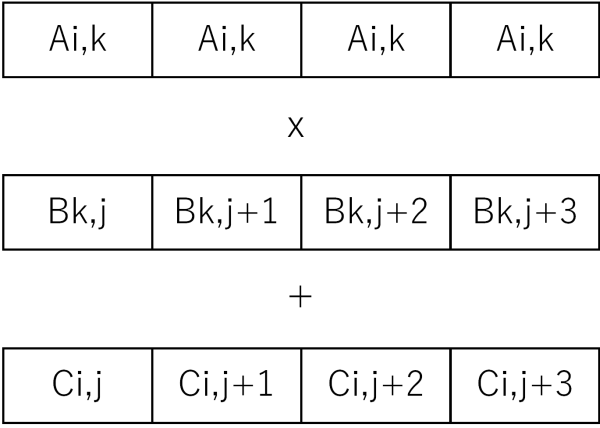
今回はSIMD命令でjの方向に一気に読むまでは同じですが、jの方向に進めるのではなく、kの方向に進めて、計算結果をCに足していく戦略です。具体的に言えばAi,kとBk,j〜Bk,j+7の8要素を一気に掛け算してCi,j〜Ci,j+7へ一気に足します。なぜ8要素かというとAVX/AVX2のレジスタ長(256bit)を使うと、32bit長のfloatを一度に8要素処理できるためです。
SIMD命令にはAi,kをSIMDレジスタの全要素に配る命令(set1_psから生成されるbroadcast命令)や、掛け算と足し算を一度に行うfmadd命令など、この計算順に最適な命令が揃っています。
AVX/AVX2のIntrinsicsの詳細についてはIntelのサイトなどを見ていただくとして(Intel Intrinsics Guide)、コードは下記のようになります。
SGEMM Intrinsics版
#include <immintrin.h>
void sgemm_avx(const float *a, const float *b, float *c, int mm, int nn, int kk)
{
for (int j = 0; j < nn;) {
if (nn - j >= 8) {
for (int i = 0; i < mm; i++) {
__m256 vc = _mm256_set1_ps(0.0f);
for (int k = 0; k < kk; k++) {
__m256 va = _mm256_set1_ps(a[i * kk + k]);
__m256 vb = _mm256_loadu_ps(&b[k * nn + j]);
vc = _mm256_fmadd_ps(va, vb, vc);
}
_mm256_storeu_ps(&c[i * nn + j], vc);
}
j += 8;
} else {
for (int i = 0; i < mm; i++) {
c[i * nn + j] = 0.0f;
for (int k = 0; k < kk; k++) {
c[i * nn + j] += a[i * kk + k] * b[k * nn + j];
}
}
j++;
}
}
}
SGEMM Intrinsics版の実行時間
$ gcc -Wall -g -O2 -static -march=znver3 sgemm.c $ ./a.out matrix size: M:1519, N:1517, K:1523 time: 0.384861 (参考: 素朴版の実行時間) time: 2.277758 (参考: ループ入れ替え版+自動ベクトル化の実行時間) time: 0.181133 (参考: OpenBLASシングルスレッドの実行時間) $ export OPENBLAS_NUM_THREADS=1 ----- use CBLAS verify: 0.052149
素朴版と比べると6倍速いですが、ループ入れ替え+自動ベクトル化には負けています。
もう少し頑張るコース - ループアンローリング
先程のコードはSIMDレジスタを3個しか同時に使っていませんでした。AVX/AVX2のYMMレジスタは16個もあるのに3個しか使わないのはもったいですから、iのループを8要素ずつアンローリングしてSIMDレジスタを同時にたくさん使いましょう。レジスタをうまく使いまわせば12要素のアンローリング(Bの保持に1個、Cの保持に12個、Aの保持に1個、計14個)まではできそうです。たぶん。
SGEMM Intrinsics+ループアンローリング版
#include <immintrin.h>
void sgemm_avx_unroll8(const float *a, const float *b, float *c, int mm, int nn, int kk)
{
for (int j = 0; j < nn;) {
if (nn - j >= 8) {
int i = 0;
for (; i < (mm & ~7); i += 8) {
__m256 vc0 = _mm256_set1_ps(0.0f);
__m256 vc1 = _mm256_set1_ps(0.0f);
__m256 vc2 = _mm256_set1_ps(0.0f);
__m256 vc3 = _mm256_set1_ps(0.0f);
__m256 vc4 = _mm256_set1_ps(0.0f);
__m256 vc5 = _mm256_set1_ps(0.0f);
__m256 vc6 = _mm256_set1_ps(0.0f);
__m256 vc7 = _mm256_set1_ps(0.0f);
for (int k = 0; k < kk; k++) {
__m256 vb = _mm256_loadu_ps(&b[k * nn + j]);
__m256 va0 = _mm256_set1_ps(a[(i+0) * kk + k]);
__m256 va1 = _mm256_set1_ps(a[(i+1) * kk + k]);
__m256 va2 = _mm256_set1_ps(a[(i+2) * kk + k]);
__m256 va3 = _mm256_set1_ps(a[(i+3) * kk + k]);
__m256 va4 = _mm256_set1_ps(a[(i+4) * kk + k]);
__m256 va5 = _mm256_set1_ps(a[(i+5) * kk + k]);
__m256 va6 = _mm256_set1_ps(a[(i+6) * kk + k]);
__m256 va7 = _mm256_set1_ps(a[(i+7) * kk + k]);
vc0 = _mm256_fmadd_ps(va0, vb, vc0);
vc1 = _mm256_fmadd_ps(va1, vb, vc1);
vc2 = _mm256_fmadd_ps(va2, vb, vc2);
vc3 = _mm256_fmadd_ps(va3, vb, vc3);
vc4 = _mm256_fmadd_ps(va4, vb, vc4);
vc5 = _mm256_fmadd_ps(va5, vb, vc5);
vc6 = _mm256_fmadd_ps(va6, vb, vc6);
vc7 = _mm256_fmadd_ps(va7, vb, vc7);
}
_mm256_storeu_ps(&c[(i+0) * nn + j], vc0);
_mm256_storeu_ps(&c[(i+1) * nn + j], vc1);
_mm256_storeu_ps(&c[(i+2) * nn + j], vc2);
_mm256_storeu_ps(&c[(i+3) * nn + j], vc3);
_mm256_storeu_ps(&c[(i+4) * nn + j], vc4);
_mm256_storeu_ps(&c[(i+5) * nn + j], vc5);
_mm256_storeu_ps(&c[(i+6) * nn + j], vc6);
_mm256_storeu_ps(&c[(i+7) * nn + j], vc7);
}
for (; i < mm; i++) {
__m256 vc = _mm256_set1_ps(0.0f);
for (int k = 0; k < kk; k++) {
__m256 vb = _mm256_loadu_ps(&b[k * nn + j]);
__m256 va = _mm256_broadcast_ss(&a[(i+0) * kk + k]);
vc = _mm256_fmadd_ps(va, vb, vc);
}
_mm256_storeu_ps(&c[i * nn + j], vc);
}
j += 8;
} else {
for (int i = 0; i < mm; i++) {
c[i * nn + j] = 0.0f;
for (int k = 0; k < kk; k++) {
c[i * nn + j] += a[i * kk + k] * b[k * nn + j];
}
}
j++;
}
}
}
SGEMM Intrinsics+ループアンローリング版の実行時間
$ ./a.out matrix size: M:1519, N:1517, K:1523 time: 0.108420 (参考: ループ入れ替え版+自動ベクトル化の実行時間) time: 0.181133 (参考: OpenBLASシングルスレッドの実行時間) $ export OPENBLAS_NUM_THREADS=1 ----- use CBLAS verify: 0.052149
もはや最適化前のコードの原型がありませんが、ループ入れ替え版+自動ベクトル化の1.7倍くらいの速度になりました。OpenBLASの1/2程度まで迫っています。この最適化手法が汎用的か?と聞かれると何とも言えないですが、SIMDレジスタを同時にたくさん使う、最内ループ以外もアンローリング(最内ループはコンパイラがやってくれる)辺りは割と汎用的なアイデアです。
あと前回言った通り、GEMMは最適化の題材として取り上げただけなので、実際にGEMMを計算する場合はこのコードや自分で書いたコードを使うのではなく、信頼と実績のOpenBLASを使ってくださいませ。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
| < | 2023 | > | ||||
| << | < | 03 | > | >> | ||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| - | - | - | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | - |
こんてんつ
 wiki
wiki Linux JM
Linux JM Java API
Java API過去の日記
 2002年
2002年 2003年
2003年 2004年
2004年 2005年
2005年 2006年
2006年 2007年
2007年 2008年
2008年 2009年
2009年 2010年
2010年 2011年
2011年 2012年
2012年 2013年
2013年 2014年
2014年 2015年
2015年 2016年
2016年 2017年
2017年 2018年
2018年 2019年
2019年 2020年
2020年 2021年
2021年 2022年
2022年 2023年
2023年 2024年
2024年 過去日記について
過去日記についてその他の情報
 アクセス統計
アクセス統計 サーバ一覧
サーバ一覧 サイトの情報
サイトの情報合計:
本日:
管理者: Katsuhiro Suzuki(katsuhiro( a t )katsuster.net)
This is Simple Diary 1.0
Copyright(C) Katsuhiro Suzuki 2006-2023.
Powered by PHP 8.2.15.
using GD bundled (2.1.0 compatible)(png support.)
 未来から過去へ表示(*)
未来から過去へ表示(*)